Numération
|
Numération
|
10. Numérisation d'une grandeur analogique(ou conversion analogique/numérique)
Exemple : numérisation de la position d'un trait sur une bande de papier
0. Découper une bande de papier d'environ 2 cm de large et exactement 20 cm de long.
1. Placer au hasard un trait sur la feuille et mesurer sa position L par rapport au bord droit de la bande de papier. Noter cette valeur.
Placer également un 1 à l'extrême gauche et un 0 à l'extrême droite.
L est la valeur analogique de la position du trait sur la bande de papier.
Diviser la bande en deux moitiés égales.
Le digit (valeur) du premier bit de la numérisation sera celui du côté où se trouve le trait. Soit le 1 dans cet exemple.
Il s'agira du rang le plus haut du convertisseur.
Ce qui donne pour l'instant : (1)2
2. Couper la bande en son milieu et reporter le digit manquant.
Ce qui donne, après avoir repéré le milieu :
Le digit du deuxième bit de la numérisation sera celui du côté où se trouve le trait. Soit le 0.
Ce qui donne pour l'instant : (10)2
3. Couper la bande en son milieu et reporter le digit manquant.
Ce qui donne
Le digit du troisième bit de la numérisation sera celui du côté où se trouve le trait. Soit le 1.
Ce qui donne pour l'instant : (101)2
4. Couper la bande en son milieu, reporter le digit manquant et repérer le milieu.
Le digit du quatrième bit est : 1
Ce qui donne : (1011)2
5. Couper la bande en son milieu, reporter le digit manquant et repérer le milieu.
Le digit du cinquième bit est : 0
Ce qui donne : (10110)2
5. Couper une dernière fois la bande en deux et relever la largeur l restante.
Analyse du résultat
La conversion a été réalisée sur 5 bits.
Ce qui représente 25 = 32 valeurs (de 0 à 31)
Ce qui signifie que la bande de papier a été divisée en 32 intervales.
La taille d'un intervalle est donc : 200 mm / 32 = 6,25 mm
position L du trait (mm) Valeur binaire correspondante Valeur décimale 0
6,25
12,5
18,75
25
31,25
37,5
43,75
50
56,25
62,5
68,75
75
81,25
87,5
93,75
100
106,25
112,5
118,75
125
131,25
137,5
143,75
150
156,25
162,5
168,75
175
181,25
187,5
193,75
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
≤ L <
6,25
12,5
18,75
25
31,25
37,5
43,75
50
56,25
62,5
68,75
75
81,25
87,5
93,75
100
106,25
112,5
118,75
125
131,25
137,5
143,75
150
156,25
162,5
168,75
175
181,25
187,5
193,75
200
00000
00001
00010
00011
00100
00101
00110
00111
01000
01001
01010
01011
01100
01101
01110
01111
10000
10001
10010
10011
10100
10101
10110
10111
11000
11001
11010
11011
11100
11101
11110
111110
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31On constate que la résolution du convertisseur sera de 6,25 mm. C'est-à-dire que la valeur numérique de la position du trait ne donnera la position exacte qu'avec une précision de 6,25 mm.
La numérisation provoque une perte d'information ou de précision.
Exemple
Soit un trait se trouvant à la position L = 155 mm
La numérisation de cette position va donner la valeur binaire 11000.
La valeur décimale correspondante est 24.
Si à partir de cette valeur on recalcul la position du trait par une règle de 3, on trouve :
L = 150 mm au lieu de 155.
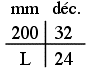
Question
Que faut-il faire pour augmenter la précision ?
Vérification
Retrouver dans le tableau ci-dessus la valeur binaire que vous avez trouvé.
Vérifier que votre position L se trouve bien dans l'intervalle donné.
Vérification par le calcul
Moodle
